El índice de Gini es un marcador que seguramente has escuchado en algún momento, probablemente te lo habrás encontrado en alguna noticia en diarios online o en algún tipo de estudio.

Este coeficiente fue creado por Corrado Gini y es cómo una manera de medir la desigualdad que existen en los países, teniendo en cuenta el nivel de ingreso. Sin embargo, no solo se limita a este uso, sino que tiene múltiples aplicaciones.
También se podría aplicar a fórmulas de medición para determinar de qué manera se distribuyen las desigualdades en los diferentes países.
La forma de representar el índice de Gini es mediante un número que puede oscilar entre el 0-1.
Vamos a estudiarlo con más detalle:
Interpretación del índice de Gini
- En el caso de que el índice de Gini fuese 0 nos estaría indicando que la igualdad es perfecta; en otras palabras, que todos los ciudadanos de un determinado lugar tienen los mismos ingresos. Por supuesto, estamos hablando de un escenario utópico que no sería posible, por lo que tan solo se podría hablar de este resultado en términos hipotéticos.
- Por el contrario, si el índice de Gini fuese 1 tendríamos la situación apuesta al caso anterior: nos habla de una desigualdad máxima en donde la riqueza no estaría nada repartida. De hecho, todo el capital sería propiedad de un único ciudadano.
Teniendo en cuenta estos dos puntos de referencia, podemos establecer las siguientes conclusiones:
- Cuánto más cerca esté el índice de Gini de 1, mayor desigualdad existirá entre los ingresos que perciben los residentes de una cierta área.
- Cuánto más cerca esté el índice de Gini de 0, mayor será la igualdad que existe entre los ingresos de una determinada área.
Ahora bien, hay que tener en cuenta que este índice podría no ser demasiado preciso en ciertas situaciones, por lo que lo más habitual es combinarlo con otros recursos, como puede ser la curva de Lorenz.
¿Cómo funciona el índice de Gini?
El método de Gini se basa fundamentalmente en la curva de Lorenz; este último recurso ayuda a representar el coeficiente de manera gráfica, para poder llegar a mejores conclusiones.
La curva de Lorez encuentra una forma de relacionar 2 variables que resultan fundamentales para entender el nivel de pobreza de una población, aunque, como ya hemos comentado, puede tener otras tantas aplicaciones.
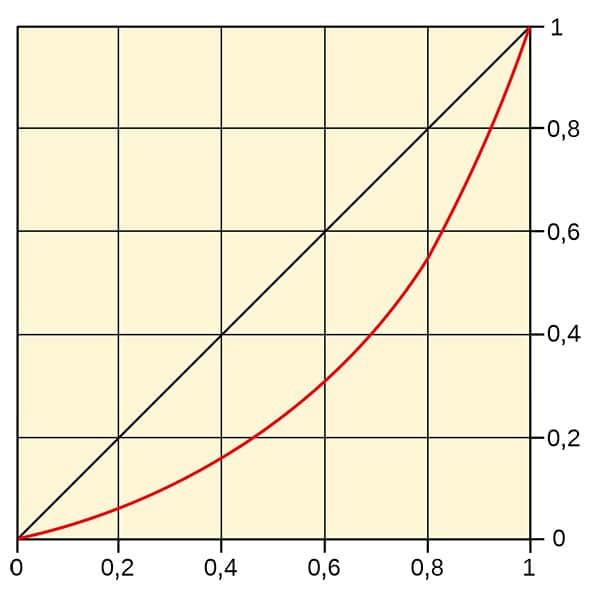
Interconecta el % de renta con el % de población de ciertas áreas. Ambos criterios se ubican en diferentes partes del plano y se van uniendo los puntos hasta que se obtiene la curva. A través de la misma, es posible conocer la evolución de los ingresos.
- Eje de las ordenadas: en el eje de las ordenadas, en el vertical, se ubicarán los datos referidos a los ingresos.
- Eje de abscisas: en el eje de las abscisas, en el horizontal, colocamos el porcentaje de la población del país al que nos refiramos. Es importante que los datos ubicados en el eje de abscisas se orden de menor a mayor renta (los de mayor renta se colocarán en la parte de la izquierda y los de mayor renta en la zona de la derecha).
Entonces extraemos conclusiones:
- Podríamos estar en la situación de encontrarnos con una línea recta, lo que sería un resultado bastante positivo. Hablaríamos de un índice de absoluta igualdad. La distribución de la riqueza en la zona sería la mejor posible; todos los habitantes de allí dispondrían de los mismos ingresos y el índice de Gini valdría 0. Habría una igualdad máxima, pero, como ya hemos comentado, estamos hablando de un escenario utópico.
- Si el resultado fuese una línea curva no muy pronunciada, nos habla de un punto intermedio. Se refiere a cuando entre el 50-60% de la población posee la totalidad de los ingresos. El índice de Gini marcaría unos valores comprendidos entre 0-1, tendería más hacia el 0.
- Si nos encontramos con una línea curva muy pronunciada, la distribución de la renta estaría en desigualdad. Hablamos de cuando más del 60% de la población tiene el 15% de la renta. El índice de Gini también lo veríamos comprendido entre el 0 y el 1, con la particularidad de que estaría más cerca del 1.
- También nos podríamos encontrar con una curva que fuese equivalente a 2 catetos del mismo triángulo. En este caso, el resultado no es nada positivo, ya que tendríamos un alto índice de desigualdad entre habitantes.
Otras referencias a tener en cuenta para estudiar el índice de Gini
Aunque el índice de Gini ofrece valores muy interesantes y exactos si se combina con la curva de Lorenz, todavía existen más conceptos que pueden ayudarnos a entender mejor estos datos y a sacar nuevas conclusiones, como los siguientes:
- Distribución de la riqueza: es posible determinar el nivel de riqueza que hay en un determinado país. Hablamos de desigualdad cuando no hay un reparto de la riqueza entre los residentes del mismo. Es posible encontrar las mayores desigualdades entre las diferentes clases sociales o jerarquías que dividen nuestra sociedad.
- Indicadores de pobreza: la pobreza se puede definir como aquel estado en el que se encuentran los individuos que no pueden acceder a aquellos recursos financieros para lograr una calidad de vida mínima. Hay muchos indicadores que se encargan de medir la pobreza, como es el caso del Índice del Desarrollo Humano, Línea de la Pobreza o el conocido Ingreso per cápita.
- Igualdad de renta: la renta no solo se refiere a un recurso monetario, también es posible medirla teniendo en cuenta los servicios/productos o los bienes con los que cuentan. Para determinar si existe o no igualdad de renta en un país habrá que tener presente las políticas económicas y sociales que se estén instaurando en el mismo.
Esperamos habernos explicado bien sobre el índice de Gini. Puedes buscar algunos ejemplos para conocer mejor su funcionamiento y su aplicación. Recuerda que, aunque se suele usar para medir las desigualdades, no es el único uso que se le puede dar.









